Indices
Fractional Indices:
Law of Indices:
How to simplify algebraic expressions
Example 1:
Example 2:
Example 3:
Logarithms
If then
. So
. For example, if
, then
, where index 4 becomes the logarithms and 2 as the base.
In general, , we call them as common logarithms (base 10). The [log] where you can find from calculator is the common logarithm.
Example 4:
Find the value of
Answer: 1.2788 [Use Calculator to find the answer]
Example 5:
Solve
Answer: m = 0.0027 [Press (shift)(log)(-2.5686)]
Laws of Logarithms:
1)
Example 6:
2)
Example 7:
3)
Example 8:
4)
Example 9:
5)
Example 10:
,
Change the Base of Logarithm
1)
2)
Example 11:
Evaluate
The following examples need to be solved using the Laws of Logarithms and change of base. So please remember the laws of logarithms and the change of the base of logarithms.
Example 12:
Find the value of
Example 13:
Simplify
Solving Equation involving indices and logarithms
a) Method 1: Expressing the equation to same base and compare the indices.
b) Method 2: Expressing the equation to same indices and compare the base.
c) Method 3: Using
d) Method 4: Expressing the equation as a single logarithms form to the same base
About the Authors:
Mr Low – A full time tutor from Malaysia, passionate about teaching Mathematics for PMR Maths, SPM Additional Maths, SPM Modern Maths and International School Maths included SAT,GCSE, Checkpoint, IGCSE syllabus.
Ms Tifeny – A full time tutor from Malaysia teaching Mathematics for SPM Additional Maths, STPM Maths and International School Maths included SAT,GCSE, Checkpoint, IGCSE syllabus, A-level, Pre-U and IB.
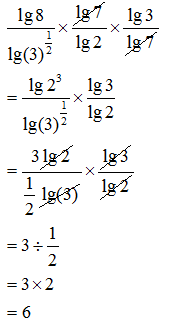
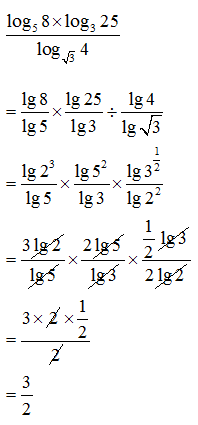
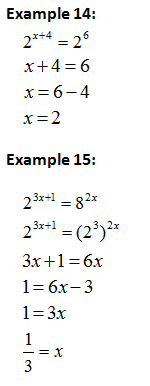
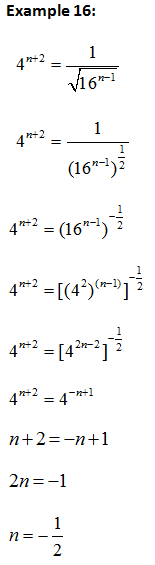
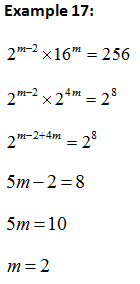
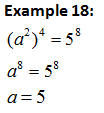
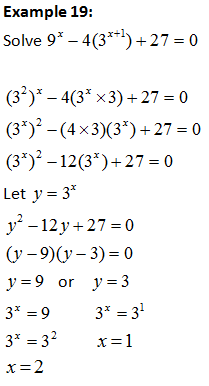

keep it up .you are fantastic
Thanks a lot you really help
Awesome
Awesome
Excellent and easy to grasp without ambiguity. Thanks
I like it
That was soo good
A well articulated program. Keep it up 💪👍