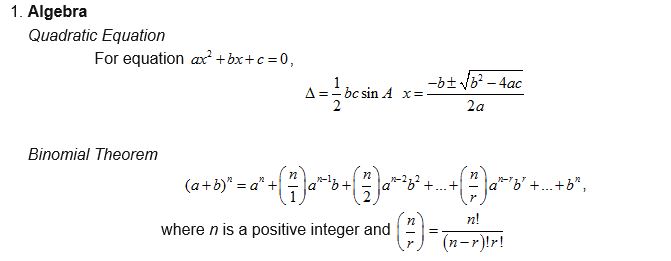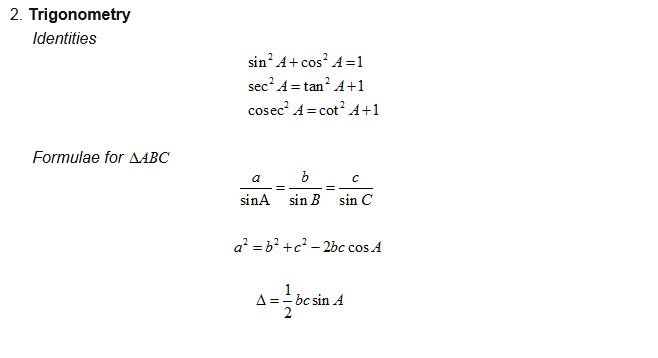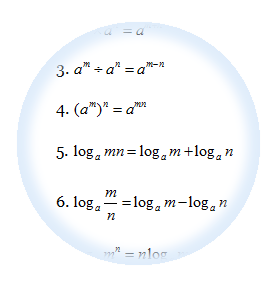Mathematics is a subject that both fascinates and challenges students of all ages. For parents, ensuring their child’s success in math is often a top priority. Home tuition is a valuable resource that can make a significant difference in a child’s mathematical journey. In this article, we’ll explore the key topics parents care about when it comes to home tuition for math.
Continue reading The Key to Math Success: Why Home Tuition Matters