These are the formulae that will be given to help you to answer the SPM Additional Maths Questions. However, more important is that you know how to apply those formulaes to solve your questions. Buy some exercises from the bookstore and work on the questions everyday and you will master all those formulaes. Basically there are divided into 5 categories:
1. Algebra
2. Calculus
3. Statistics
4. Geometry
5. Trigonometry
Algebra
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Calculus
1.
2.
3.
4. Area under a curve =
5. Volume generated =
Statistics
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12. Mean/Min
13.
14.
Geometry
1. Distance =
2. Midpoint
3. A point dividing a segment of a line
4. Area of a triangle =
5.
![]()
6.
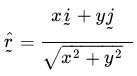
Trigonometry
1. Length of an arc,
2. Area of a sector,
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14. Area of a triangle =
You could also download the pdf version here: SPM Additional Mathematical Formulae-pdf
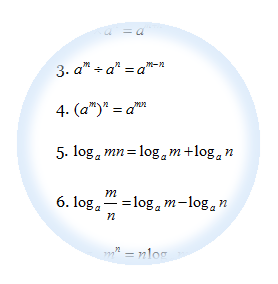
for the algebra, is it algebra 1 or 2 or 3? or all 3?
This is just the exact formulae sheet that will be given in spm exam.
It is very useful